Melody analysis: class statistics
The idea is: Are there peculiarities in the style of a composer (or a piece or a period) that can be measured with our mathematical method? Have certain composers preferences for certain motif classes? Or does one composer write melodies with many different classes and another composer only with few?
Deeper going analyses were not possible within the scope of this thesis (and with the limited equipment I disposed of at that time - there was plenty of computer power but it is only now that I have easy access to musical data via MIDI. I would like to redo it now when I find the time). I can only present a few examples that are far from allowing to derive universally valid statements; but in any case they raise some questions and show some of the problems.
Assuming the data are there in form of a MIDI file - how do we extract the motifs? A first idea (and actually the approach I took) could be to consider all sequences of n immediately succeeding tones as motifs (with n elements - every 2 such motifs have n-1 tones in common). This method is easy to implement, but on one hand it produces a certain amount of noise because it ignores phrasing, and on the other hand certain motifs will not be found - as e.g. a motif formed by the bass line of an arpeggio. The "correct" way (if there is "the" correct way at all) would be to identify the musical phrases - a definitely non-trivial task that enters an additional dimension of complexity if the original score is, say, a piano part where the voices have to be extracted first. This is another fascinating research field - but (like other things) it is out of the scope of this work. (In the RUBATO workstation similar algorithms have been realized.)
As examples for melody analysis I chose: the Sarabande (3/4 measure) and the first part of the Gigue (12/16 measure) from the French Suite in G mayor by J. S. Bach (BWV 816), the beginning of the Piano part in the first movement (3/4 measure) of the Piano concerto in E flat major by W. A. Mozart (KV 449), the main theme and an organ solo over it in the title piece of "Sarabande" by Jon Lord (Purple records 1976). This choice already reflects one weakness of the algorithm (not the basic approach but the current realization): its restriction to 12-measures. For serious applications, the generalization to arbitrary measures would be one of the first things to be done.
In Bach's sarabande I encountered another problem: The major part of the piece contains no time values smaller than 16th, yet there are some passages where 32ths and triplets are used - thus not suiting into the 12-beat bar! This is the same problem as above - I evaded it this time by omitting a few tones. But assumed this is solved or we work in Z^2 - should we really refine the time subdivision for the whole piece, thus multiplying ALL time coordinates by a certain value? First, this looks like "overkill". Second, in Z^2 this is a non-invertible transformation; hence all classes will be labeled differently! (In Z12xZn we are not even sure yet what exactly the onsequences will be.) Obviously the classes we have derived are not to be taken "absolutely" but relative to a certain subdivision - a subdivision that also could change inside one piece. For the case of Z^2, it seems that including non-invertible affine transformations might be the better classification since we gain acertain independence of the subdivision.
Conclusion: There is still a way to go until we can do serious analyses!
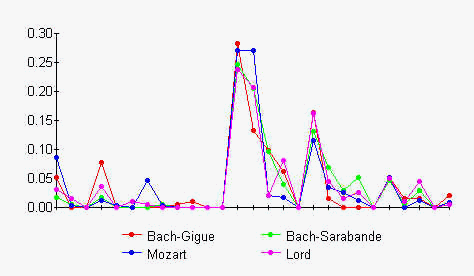
Given these restrictions, here are the results (quotas) for 3-element motif classes.
 .
.
At first sight, the distributions of motifs with 3 elements look rather similar: in the analyzed parts of all 4 pieces the classes 12, 13 and 17 occur most often, class 12 being the leader; in the analyzed parts of all 4 pieces there are no occurrences of the classes 2, 4, 7, 8, 10, 11, 16, 21 and 25. But since we know about the non-equal distribution of the classes, we can see this as normal. Weighting every result against its probability might give a clearer picture.
To my untrained eye, the 2 sarabandes look most alike, and the piece by Mozart most different from the rest. We would have to use statistical tools to obtain qualifiable results. And - I repeat - we really need much more data, i.e. analyses of various pieces by many different composers, before we can make statements with a certain level of validity. A possible result might be that the melodic structure of Jon Lord's "Sarabande" is indeed quite close to its baroque models.
Algorithmic composition
If the here presented methods allow to analyze musical pieces and extract stylistic peculiarities of the compositional style of a composer, is it then also possible to let a computer generate a piece in the style of this composer?
What I tried was the following: Given a sequence of isomorphy classes (e.g. one obtained from an analysis like in the previous chapter), I let the computer generate random pitch and note-on time values. As soon as a motif has been generated that way, its isomorphy class is calculated. If it coincides with the class of the corresponding motif (the n-th motif is the motif whose first tone is tone n of the whole melody), we continue with the next motif, else the generated tone is discarded (but kept in memory to prevent creation the same note again and again).
Observe first that if the isomorphy classes of the motifs are the only criterion upon which a melody is built, the result will almost certainly be absolutely disgusting. To get results you can at least listen to, I had to build in a bunch of other constraints, such as restriction of the pitches to a given major or minor scale, preference of short time intervals, always a note on the first beat of a measure. What this shows is that the structures we are describing method already reside on a certain level of abstraction and should be taken into consideration only after some "basic work" has been done - a human composer usually proceeds in an analogous way.
I admit the whole approach is rather "brute force" - and, as you will hear, it sounds like that. But when you listen, keep in mind that our method is based on just a little part of musical reality - from the vast variety of parameters we consider only two (beginning time and pitch), and moreover: even within these parameters there are important musical structures such as rhythm, harmonies, modulations, phrasing, syntax that we ignore almost completely. Taking into account these reservations, I still got the (possibly biased) feeling that some of the characteristics of the original melodies can be heard...
Original 1: J. S. Bach, French suite in G major (BWV 816), beginning of the first voice of the Gigue.
2 computer-generated melodies with the same isomorphy classes
of 3-element motifs.
Melody 1(major), melody
2 (harmonic minor).
Computer-generated melodies with the same isomorphy classes of
4-element motifs. Observe that the rhythm in the second example
is exactly like in the original.
Melody 1, melody 2.
Computer-generated melodies where all motifs are isomorphic to
the same motif (the first of the original).
Melody 1, melody
2.
There indeed seems to be less "progression", does it
not?
Original 2: W. A. Mozart, Piano concerto in E flat major (KV 449), beginning of the piano part.
Computer-generated melodies with the same isomorphy classes of
4-element motifs.
Melody 1, melody 2.
The results seems worse than for Bach - partly because of the
larger time values (but the original contains them, too...)