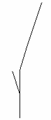1. Einleitung 2. Fraktale und Natur 3. Programmieren von Fraktalen 3.1. Die Programmiersprache C++
3.2. Pythagorasbaum 3.2.1. Mutation 1 3.2.2. Mutation 2 3.3. Astbaum 3.4. Lindenmayer System
3.4.1. Einführung 3.4.2. Programm 3.4.3. Eigene Beispiele 4. Nachwort 5. Ehrlichkeitserklärung
Literaturverzeichnis und Internetadressen
3.4. Lindenmayer System
3.4.1. Einführung
Der Biologe Aristid Lindenmayer hat 1968 ein System entwickelt, um das Wachstum von Pflanzen zu beschreiben. Ein solches System wird L-System oder Lindenmayer System genannt. ¹
Ein Fraktal wird im L-System durch Zeichenfolgen beschrieben. Dazu gehören ein Startterm
und mindestens eine Umwandlungsfunktion. Die Umwandlungsfunktionen definieren, wie in jedem Iterationsschritt einzelne Zeichen durch Zeichensequenzen ersetzt werden. Nach n Iterations-schritten wird die gebildete Zeichensequenz grafisch interpretiert. Dabei haben nur folgende Zeichen eine Bedeutung:
Tab. 3
Zeichen
Interpretation des Zeichens
F
Zeichne eine Linie mit einer vorgegebenen Länge in Richtung d
!
Bewege dich um eine vorgegebene Länge in Richtung d ohne zu zeichnen
+
Drehe dich um den Winkel a gegen den Uhrzeigersinn.
-
Drehe dich um den Winkel a im Uhrzeigersinn
[
Merke dir die aktuelle Position und Richtung
]
Gehe zurück zur zuletzt gemerkten Position und Richtung
Alle anderen Zeichen werden für die grafische Ausgabe ignoriert.
Um das Lindenmayer System zu verstehen, wenden wir es an einem bekannten Fraktal, der Koch-Kurve, an. Die Koch-Kurve wird im L-System folgendermassen beschrieben:
Startterm: F
Umwandlungsfunktion: F -> F+F--F+F
Winkel a: 60°
Startrichtung: 0° (Dies bedeutet, dass die Richtung d zu Beginn 0° ist.)
Die vorgegebene Länge ist an sich willkürlich und wird zunächst vom Programm in bestimmter Weise festgesetzt. Sie kann später im Programm vom Benutzer festgelegt werden.
Tabelle 4 zeigt die entstehende Zeichensequenz nach 0, 1 und 2 Iterationsschritten.
Tab. 4
Iterationsschritte
Zeichensequenz
0
F
1
F+F--F+F
2
F+F--F+F+ F+F--F+F--F+F--F+F+ F+F--F+F
Durch das wiederholte Anwenden der Umwandlungsfunktion wächst die Länge der Zeichenfolge rasch an, da jedes Mal alle F durch F+F--F+F ersetzt werden.
Tabelle 5 zeigt die dazugehörigen grafischen Darstellungen.
Dabei ist zu beachten, dass in diesen Darstellungen die vorgegebene Länge von Figur zu Figur abnimmt.
Tab. 5
Iterationsschritte
Grafische Ausgabe
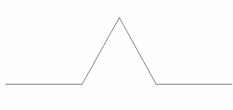
0
1
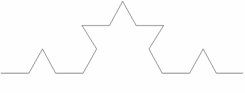
2
Abbildung 20 zeigt die Koch-Kurve nach 5 Iterationen.
Abb. 20
Eine Koch-Schneeflocke besteht sozusagen aus drei Koch-Kurven, die in einem gleichschenkligen Dreieck aneinandergehängt sind.
Der Startterm muss dabei geändert werden zu F--F--F.
Dies bewirkt, dass pro Iteration zuerst eine Koch-Kurve gezeichnet wird, diese um 120 Grad im Uhrzeigersinn gedreht wird, eine zweite Koch-Kurve gezeichnet wird, welche wieder um -120° gedreht wird und ein letztes Mal die Kurve gezeichnet wird.
Das Ergebnis nach 4 Iterationen zeigt Abbildung 21.
Abb. 21
Ein zweites, eigenes Beispiel zeigt die Anwendung der Klammern [ und ]:
Startterm: F
Umwandlungsfunktion: F -> F[+F]F[-FFF]
Winkel a: 18°
Startrichtung: 90°
Tabelle 6 zeigt die Zeichensequenz, Tabelle 7 die grafische Ausgabe nach 0-2 Iterationsschritten.
Tab. 6
Iterationsschritte
Zeichensequenz
0
F
1
F[+F]F[-FFF]
2
F[+F]F[-FFF][+ F[+F]F[-FFF]] F[+F]F[-FFF][-F[+F]F[-FFF] F[+F]F[-FFF] F[+F]F[-FFF]]
Iterationsschritte
Grafische Ausgabe
0
1
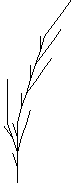
2
Tab. 7
In dieser Tabelle wird ebenfalls die Seitenlänge s von Figur zu Figur minimiert.
Abbildung 22 zeigt diese Pflanze nach 5 Iterationen:
Abb. 22
Wie schon erwähnt, können auch mehrere Ersetzungsregeln angegeben werden und noch andere Zeichen als die, die für die grafische Ausgabe relevant sind, verwendet werden.
Dies soll an einem dritten, eigenen Beispiel gezeigt werden.
Folgende Parameter beschreiben das Wachstum eines Baumes:
Startterm: WK
K -> [++WK]W[--WK]W[+WK][-WK]
W -> WF
Winkel a: 15°
Startrichtung: 90°
Die Buchstaben W und K stehen für Wachstumszone und für Knospe. Bei jeder Iteration werden K und W durch die gegebenen Zeichenfolgen ersetzt.
Die folgenden Abbildungen stellen den Entwicklungsprozess des Baumes dar:
Startterm:
Abb. 23
Nach 1. Ersetzung:
Abb. 24
Nach 2. Ersetzung:
Abb. 25
Die Rechtecke stehen hier für die Wachstumszone (W) und die Ellipsen stehen für die Knospen (K). Der Startterm besteht aus einer Wachstumszone mit einer Knospe. Nach der 1. Iteration werden aus der Wachstumszone ein F, welches hier schwarz dargestellt ist, sieben neue Wachstumszonen und vier Knospen. Im nächsten Schritt entstehen aus diesen Wachstumszonen wieder Fs (schwarze Rechtecke).
So wird ein Wachstumsprozess beschrieben. Je weiter verzweigt die Äste sind, desto kürzer sind sie. In jeder Iteration wachsen alle Äste.
Die nächsten Abbildungen zeigen die grafische Ausgabe nach der 1., 2. und 5. Ersetzung. Die Seitenlänge ist dabei in Abbildung 26 gleich gross wie in Abbildung 27. In Abbildung 28 ist sie verkürzt.
Abb. 26
Abb. 27
Abb. 28
¹ Heiz-Otto Peitgen; Hartmut Jürgens; Dietmar Saupe. Chaos; Bausteine der Ordnung. Klett-Cotta. 1994.